- Cost planning
- Cost Analysis
- Cost management Techniques
- Externally oriented Cost Management Techniques
- Relevant costs
- Short term decisions
- Risk and Uncertainty
- Linear programming – graphical method
- Linear programming the simplex method
- Multi Product CVP Analysis
- Pricing decisions and Pricing strategies
- Budgetary Control
- Performance Evaluation
- Measuring performance in divisionalised businesses
- Transfer pricing
The Simplex Method – using computer
The simplex method is of particular use because it is able to consider more complex problems involving more than two output variables. This is an iterative (or repetitive) process that calculates the contribution at each vertex of the feasible region, starting with the origin. The process is normally carried out by a computer which will provide not only an optimal solution but also a sensitivity analysis for the data.
There are three stages:
- Preparing the input for the computer (or a manual solution). We do this in the form of a table or tableau, known as the initial tableau.
- The computer processes the data by means of a series of matrix multiplications.
- The computer produces the output in the form of a final tableau and we have to interpret the information.
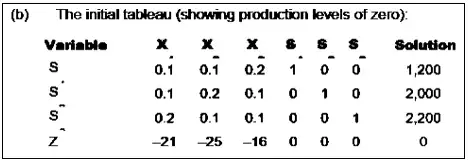
Setting up the initial tableau
The initial tableau shows the production problem when the output of all the products is zero. It is like considering the origin of the graph. In order to produce the first tableau it is necessary to convert each inequality into an equation. This is done by introducing a slack variable for each constraint.
Let S1 = Slack in Department A
Let S2 = Slack in Department B
Let S3 = Slack in Department C
Having written the equations, it is now possible to produce the initial tableau:
| Variable | X | Y | S1 | S2 | S3 | Solution |
| S1 | ||||||
| S2 | ||||||
| S3 |
Contribution
The contributions per unit should be entered as negative numbers. This is just a feature of the mathematics and has to be remembered as a rule.
Interpreting the final tableau
The computer processes the data contained in the initial tableau and it produces the final tableau.
*In the examination, the final tableau will always be given. You must be able write a full interpretation of the output.
Test your understanding
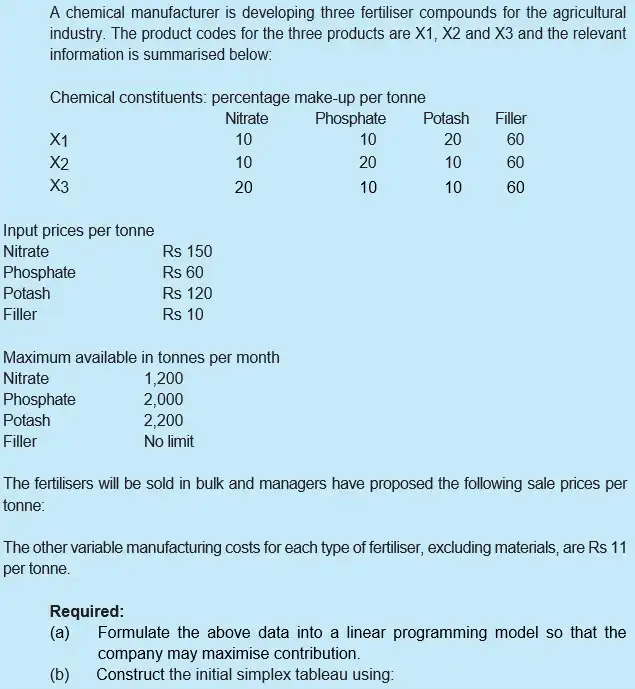

Solution
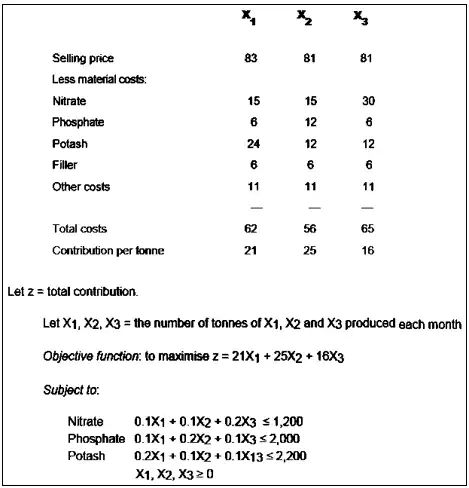
(c) The optimum monthly production plan is: 4,000 tonnes of X1 and 8,000 tonnes of X2. Zero tonnes of X3 should be produced.
The maximum monthly contribution is Rs 284,000. This contribution would fall by Rs 22 for each tonne of X3 that was produced.
The nitrate and phosphate are both fully utilised, their slack is zero. If additional tonnes of these chemicals could be obtained then contribution would increase by Rs 170 per tonne of nitrate and by Rs 40 per tonne of phosphate. There is slack of 600 tonnes of potash.
Additional information revealed by this final tableau:
- If one additional tonne of nitrate were to become available production of X1 should increase by 20 tonnes and production of X2 should decrease by 10 tonnes. This alteration to the mix will increase contribution by Rs 170. The slack of potash will fall by 3 tonnes.
- If one additional tonne of phosphate were to become available production of X1 should decrease by 10 tonnes and production of X2 should increase by 10 tonnes. This alteration to the mix will increase contribution by Rs 40. The slack of potash will increase by 1 tonne.
- If one tonne of X3 must be manufactured contribution will decrease by Rs 22. The mix must be altered in order to make one tonne of X3; Production of X1 must decrease by 3 tonnes and production of X2 must increase by 1 tonne. The slack of potash will increase by 0.4 of a tonne.
